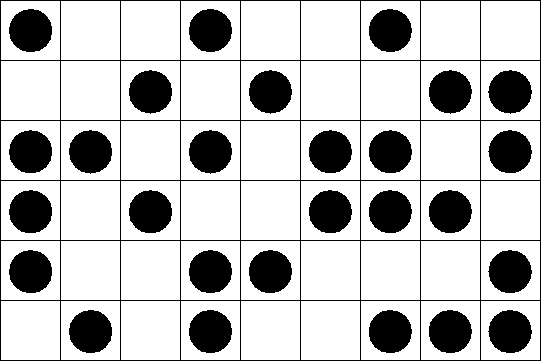
Каждая ячейка либо занята, либо пуста. Только ближайшие соседи могут взаимодействовать. Энергия взаимодействия
Назад: Фазовые переходы в модели Изинга
Дальше:
Заключение
Модель Изинга была изобретена, чтобы описать фазовый переход в магнетике. Но она также описывает и другие важне явления, например фазовый переход жидкость-пар!
Рассмотрим такую

Каждая ячейка либо занята, либо пуста. Только ближайшие соседи могут
взаимодействовать. Энергия взаимодействия
![]() .
Свяжем это с моделью Изинга. Введем соответствующий частицам "спин"
.
Свяжем это с моделью Изинга. Введем соответствующий частицам "спин"
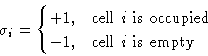
и, наоборот, сопоставим спинам обычной модели Изинга "частицы"
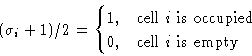
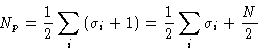
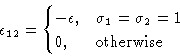
![]()
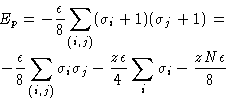
| |
(2) |
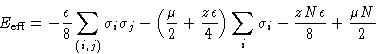
![]()
| Магнетик Изинга | Газ на решетке |
| Канонический ансамбль | Большой канонический ансамбль |
| Взаимодействие (константа связи) J | Энергия взаимодействия |
| Внешнее поле H | Химпотенциал |
| Намагниченность M | Плотность |
| Свободная энегрия A | |
| Восприимчивость |
Сжимаемость |
| Изотропная фаза | Суперкритическая жидкость |
| Анизотропная фаза | Жидкость или газ |
| Точка Кюри | Критическая точка |
Рассмотрим несжимаемую смесь жидких A и B:
Снова взаимодействуют только ближайшие соседи. Энергия взаимодействия:

Снова введем значение "спина", соотвестсвующего такой системе:
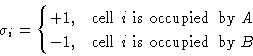
![]()
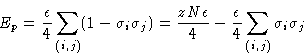
![]()
Здесь никак не используешь большой канонический ансамбль, так как полное число частиц сохраняется (есть несжимаемость). Рассмотрим "полубольшой ансамбль" ("Semi-Grand Ansamble"): полное число частиц фиксированно, но but можно менять соотношение между A и B.
Статсумма при этом:
![]()
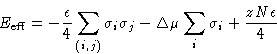
![]()
Аналогия между Изинговским магнетиком и бинарным раствором:
| Магнетик Изинга | Бинарный раствор |
| Канонический ансамбль | "Полубольшой" ансамбль |
| Взаимодействие (константа связи) J | Энергия взаимодействия |
| Внешнее поле H | Разность химпотенциалов компонент |
| НамагниченностьM | Composition |
| Разупорядоченная фаза | Фаза раствора |
| Упорядоченная фаза | Фаза расслаивания веществ А и В |
| Точка Кюри | Критическая точка расслаивания |
Каково дальнейшее развитие модели Изинга?
Назад: Фазовые переходы в модели Изинга
Дальше:
Заключение