Назад: Модель Дальше: Применение модели Изинга

Фазовые переходы в модели Изинга

Нет внешнего поля. Точка Кюри.

Пусть H=0 (нет выделенного направления в пространстве - симметричный случай). Энтропия пытается разупорядочить спины, но параллельные состояния более энергетически выгодны.

При больших T побеждает энтропия: M=0
При малых T перебарывает энергия: $M=\pm1$
В пограничной точке - точке Кюри T_c - имеет место фазовый переход. Это переход второго рода (почему?).

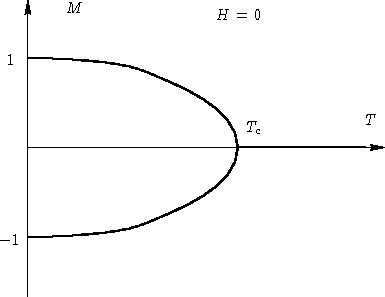
$\begin{figure} \psfrag{1}{$1$} \psfrag{-1}{$-1$} \psfrag{M}{$M$} \psfrag{T}{$T$} \psfrag{Tc}{$T_c$} \psfrag{H=0}{$H=0$} \includegraphics{MT}\end{figure}$

Ненулевое внешнее поле. Восприимчивость.

Если $H\ne0$ , намагниченность M параллельна H. Существует некая функция M(H,T). Что происходит если $H\to0$ ?

При T>T_c, система разупорядочена если H=0:
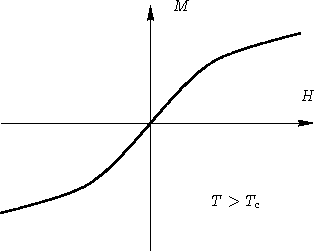
$\begin{figure} \psfrag{H}{$H$} \psfrag{M}{$M$} \psfrag{T\gt Tc}{$T\gt T_c$} \includegraphics{MH_highT} \end{figure}$

$\begin{displaymath} \lim_{H\to0} M(H,T)=0,\quad T\gt T_c \end{displaymath}$
При T<T_c, система упорядочена при H=0:
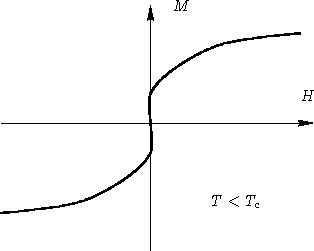
$\begin{figure} \psfrag{H}{$H$} \psfrag{M}{$M$} \psfrag{T<Tc}{$T<T_c$} \includegraphics{MH_lowT} \end{figure}$

$\begin{displaymath} \lim_{H\to\pm0} M(H,T)=\pm M_0(T),\quad T<T_c \end{displaymath}$
При T приближающейся к T_c, вертикальная часть предыдущего графика сокращается, так что в точке фазового перехода рассматриваемая функция уже непрерывна, но ее наклон все еще вертикален - производная бесконечна!
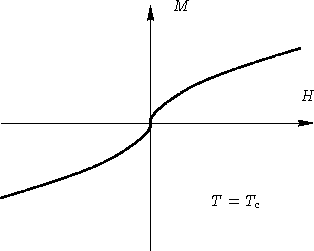
$\begin{figure} \psfrag{H}{$H$} \psfrag{M}{$M$} \psfrag{T=Tc}{$T=T_c$} \includegraphics{MH_critT} \end{figure}$

$\begin{displaymath} \lim_{H\to\pm0} M(H,T)=0,\quad \lim_{H\to0} \frac{\partial M(H,T)}{\partial H} = \infty, \quad T=T_c \end{displaymath}$

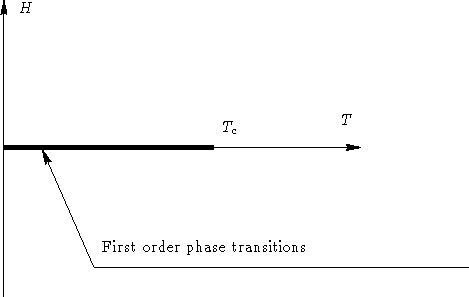
В критической точке восприимчивость системы бесконечна!

Так как амплитуда флуктуаций порядка

$\begin{displaymath} \left\langle (\Delta M)^2\right\rangle = \frac{\chi kT}{V}\end{displaymath}$

флуктуации бесконечно растут T_c!

Все это можно изобразить на фазовай диаграмме:

Назад: Модель Дальше: Применение модели Изинга