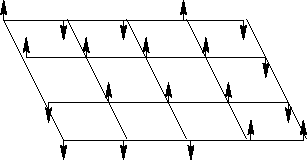
Пусть рассматриваются N спинов $\sigma_i$ , i=1, 2,... на решетке, каждый может быть направлен либо вверх, либо вниз:

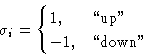
$\begin{displaymath} \sigma_i = \begin{cases} 1,& \text{``up''}\ -1,& \text{``down''} \end{cases}\end{displaymath}$

$\begin{figure} \includegraphics{ising}\end{figure}$

Энергия:

1.

Каждый спин взаимодействует с внешним полем H:

$\begin{displaymath} E_1 = -H\sum_i \sigma_i \end{displaymath}$

2.

Спины, ближайшие друг к другу также взаимодействуют:

(a): Параллельно выстраиваться спинам "выгодно" - этому соответствует энергия -J, J>0
(b): Антипараллельные спины энергетически невыгодны - на образование каждой такой пары требуется положительная энергия +J

Энергию взаимодействия каждой пары можно записать в виде $-J\sigma_1\sigma_2$ . Тогда полная энергия системы:

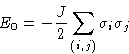
$\begin{displaymath} E_0 = -\frac{J}{2}\sum_{(i,j)}\sigma_i\sigma_j \end{displaymath}$

Здесь (i,j) обозначает суммирование по парам ближайших соседей

В результате:

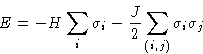$\begin{displaymath} E = -H\sum_i \sigma_i -\frac{J}{2}\sum_{(i,j)}\sigma_i\sigma_j\end{displaymath}$

(1)

Статсумма и термодинамические переменные

Микроскопическое состояние системы задает набор всех спинов:

$\begin{displaymath} \{\sigma\} = \{\sigma_1,\sigma_2,\dots\}\end{displaymath}$

Тогда статсумма - сумма по всем этим состояниям:

$\begin{displaymath} Z_N = \sum_{\{\sigma\}} \exp\bigl(-\beta E(\{\sigma\})\bigr)\end{displaymath}$

Обратите внимание, здесь нет зависимости от импульсов (нет кинетической энергии) - т. е. это скорее конфигурационный интеграл чем статсумма! Свободная энергия равна:

$\begin{displaymath} A = -kT\ln Z_N\end{displaymath}$

Средняя намагниченность равна (говорят, что H и $N\sigma$ сопряжены, так как домножение на одну из этих величин под знаком усреднения можно заменить на дифференцирование по другой величине - усреднение обозначает свертку с функцией распределения, а та всегда содержит экспоненциальный множитель exp(-E).)

$\begin{displaymath} M(H,T) = \left\langle \sigma\right\rangle = -\frac{1}{N}\frac{\partial A(H,T) }{\partial H}\end{displaymath}$

Восприимчивость:

$\begin{displaymath} \chi = \frac{\partial M(H,T) }{\partial H} = -\frac{1}{N}\frac{\partial^2 A(H,T) }{\partial H^2} \ge 0\end{displaymath}$

Энергия:

$\begin{displaymath} E = A - T \frac{\partial A(H,T) }{\partial T} = -T^2 \frac{\partial A(H,T)/T }{\partial T} \end{displaymath}$

Теплоемкость:

$\begin{displaymath} C = \frac{\partial E(H,T) }{\partial T}\end{displaymath}$

Назад: Оглавление Дальше: Фазовый переход в модели Изинга

Модель Изинга

Гамильтониан и статсумма модели Изинга

Энергия:

Статсумма и термодинамические переменные