Мицеллообразование

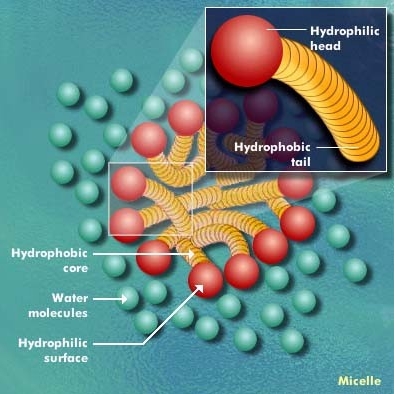Мицеллы – это наноразмерные относительно устойчивые агрегаты из молекул поверхностно-активных веществ (ПАВ), которые самопроизвольно образуются в растворах ПАВ. При повышении брутто-концентрации раствора (т.е. полного количества ПАВ в единице объема раствора) выше первой критической концентрации мицеллообразования (ККМ) доля мицелл в балансе ПАВ в растворе становится уже существенной. На сегодняшний день область применения мицеллярных (т.е. содержащих значительное число мицелл) растворов огромна. Они используются в моющих средствах и для создания микроэмульсий, при добыче полезных ископаемых и нефти. В то же время в океане мировой литературы по мицеллярным растворам лишь небольшой процент приходится на кинетику агрегации в мицеллярных растворах, что объясняется исключительной сложностью процессов мицеллообразования. Первые исследования кинетики мицеллообразования были стимулированы фактом экспериментального наблюдения времен быстрой и медленной релаксации мицеллярного раствора со сферическими мицеллами. Предложенный Анианссоном подход на основе представлений о пошаговом росте мицелл, аналогичном росту зародышей новой фазы в процессах нуклеации, получил широкое распространение и применялся затем для описания более сложных систем. Исходя из идеи о барьерном характере процесса агрегации в мицеллярных растворах, данный подход, однако, не использовал в полной мере возможности теории нуклеации в установлении связи между основными характеристиками процесса агрегации, свойствами молекулярных агрегатов разных размеров, параметрами начального и конечного состояний мицеллярного раствора. Поскольку о предмицеллярных агрегатах, в особенности, о тех, которые можно назвать критическими зародышами мицелл, было мало экспериментальных данных, то дальнейшее развитие кинетики агрегации в мицеллярных растворах затормозилось.

В последнее время интерес к кинетике мицеллообразования вновь возрос. Появились работы, в которых пошаговая схема кинетики агрегации, основанная на кинетическом уравнении Беккера-Дёринга, анализировалась на предмет необратимого поведения и устойчивости решения и была предложена процедура сокращения описания, позволяющая оптимизировать алгоритмы численного решения системы кинетических уравнений агрегации. Было достигнуто продвижение и в теории нуклеации, в частности, в решении проблем кинетики ион-индуцированной нуклеации и кинетики гетерогенной нуклеации на смачиваемых частицах , которые оказались родственны проблемам кинетики мицеллообразования.

Построение кинетической теории мицеллобразования в растворах ПАВ на основе теории нуклеации нуждается в знании из термодинамики работы образования молекулярного агрегата ПАВ (работы агрегации). Существуют две термодинамические модели мицеллы: капельная и квази-капельная. В ситуации, когда брутто-концентрация ПАВ превышает первую ККМ, однако, лежит ниже второй ККМ, начиная с которой заметная доля ПАВ будет накапливаться уже в цилиндрических мицеллах, эти модели показывают, что работа агрегации, как функция числа агрегации молекулярных агрегатов, имеет не только потенциальный горб, но и лежащую правее него на оси чисел агрегации потенциальную яму, за которой работа растет неограниченно. Существование потенциального горба и потенциальной ямы работы агрегации вносит усложнения в кинетическую теорию мицеллообразования по сравнению с кинетической теорией гомогенной нуклеации, которая исходит из того, что работа образования зародыша возникающей фазы обладает как функция числа его молекул лишь потенциальным горбом, за которым она уже монотонно спадает. Еще более сложна ситуация, когда брутто-концентрация ПАВ превышает вторую ККМ, когда все большую роль начинают играют цилиндрические мицеллы, и в работе агрегации появляются дополнительный потенциальный горб и потенциальная яма.

Как и в кинетической теории нуклеации, в кинетической теории мицеллообразования важным является поток молекулярных агрегатов, преодолевающих флуктуационно потенциальный горб работы их образования со стороны области, лежащей левее горба. Однако, поскольку в мицеллярном растворе за потенциальным горбом следует потенциальная яма, а не монотонное спадание работы агрегации, то в кинетической теории мицеллобразования важным является ещё и поток молекулярных агрегатов, преодолевающих флуктуационно потенциальный горб работы их образования со стороны потенциальной ямы. Нахождение прямого и обратного потоков молекулярных агрегатов через потенциальные горбы работы агрегации играет принципиальную роль в построении кинетики агрегации в мицеллярных растворах и анализе стадий мицеллообразования. При этом важными задачами являются описание с кинетических позиций релаксации мицеллярного раствора и установление иерархии характерных кинетических времен мицеллообразования. Иерархия дает наглядное представление об относительных величинах времён возникновения и распада мицелл и сложного многостадийного процесса приближения мицеллярного раствора к финальному состоянию равновесия.

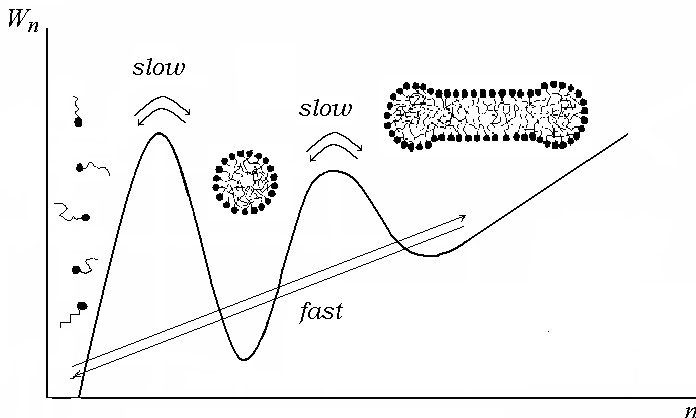
Иллюстрацией к свойствам мицеллярных растворов может быть следующий рисунок. Здесь 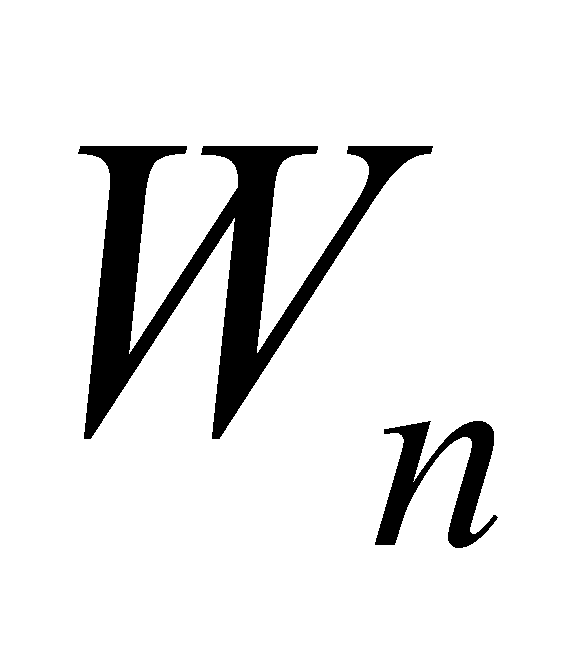– это выраженная в тепловых единицах 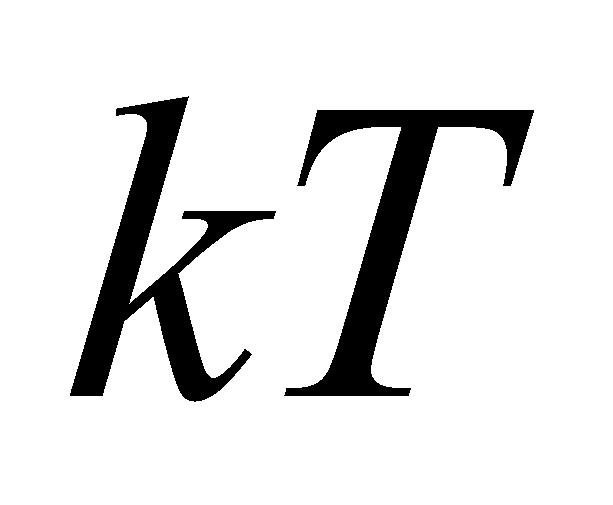(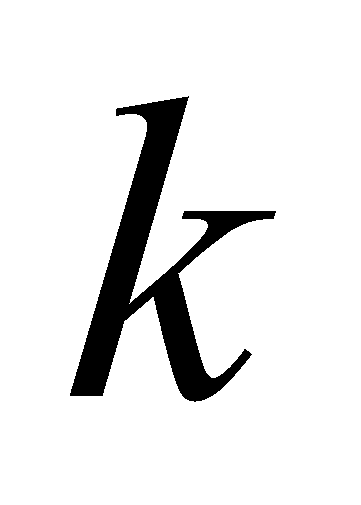– постоянная Больцмана, – абсолютная температура) работа образования агрегата из молекул ПАВ при брутто-концентрации выше второй ККМ. Показаны области мономеров ПАВ, сферических и сфероцилиндрических мицелл. Стрелками показаны переходы, соответствующие быстрым и медленным процессам в мицеллярном растворе.