Nucleation
Various first-order phase transitions, from the commonest (e.g. condensation of liquid droplets in a supersaturated vapour) to latent pore formation from a supersaturated vacancy solution in a solid, occur in virtually identical stages, the starting point being the creation of a metastable state of matter. The transformation of matter to a metastable state, such as the production of a supersaturated vapour, superheated and supercooled liquids or supersaturated solutions is possible in different ways. In practice, all of them are categorized into two groups depending on how rapidly the physical parameters of a substance are changed by factors which induce metastable state formation. By the instantaneous formation of metastability is meant the transition to a metastable state during a time much smaller than the characteristic time of subsequent phase transition. The gradual formation of metastability occurs in the opposite situation when factors responsible for matter transformation to a metastable state and going further into the metastability region remain active after the intense phase transition has begun.
The knowledge of metastable state characteristics immediately after its instantaneous formation, when it is not yet perturbed by the subsequent phase transition, considerably simplifies the theory describing the progress of phase transition under such conditions. This explains to a large extent why the majority of theoretical and experimental works now recognized as classical proceeded from the assumption of instantaneous formation of the initial metastable state.
Considerable progress in the description of phase transitions under the gradual formation of metastability has been achieved during the last two decades. Theoretical studies have demonstrated that, if certain weak constraints are imposed on the metastability formation rate, two conspicuous stages can be distinguished in the course of a phase transition. The initial one is the nucleation stage giving rise to the bulk of steadily growing nuclei of the new, stable phase. The non-linearity of nucleation manifest as the strong dependence of the intensity of formation of stable phase nuclei (nucleation rate) on the degree of metastability at the initial stage accounts for the short duration of the nucleation process compared with the characteristic time of metastable state formation. This stage is induced by metastability-forming factors while its termination depends on a decrease in metastability (despite the continuing action of the causative factors) due to the transfer of a fraction of the matter from the metastable phase onto the stable phase nuclei. In the beginning, this fraction is small. The metastable phase almost entirely shifts to the stable one after the termination of the nucleation stage and the onset of the so-called collapse stage. This stage is characterized by the further growth of stable phase nuclei without a substantial change in their numbers. The intensity of the action of factors creating metastability, the number of new phase nuclei formed at the nucleation stage and their growth rate (the rate of utilization of metastable phase matter by the nuclei) are interrelated such that practically all the matter rapidly shifts to the stable state at the collapse stage. In the case of an additional constraint imposed on the metastability formation rate, the collapse stage is followed by the well-known Ostwald ripening stage during which large particles of the new phase grow on account of disappearing small ones.
Ostwald ripening had been described (by the theory of Lifshits-Slezov) before the theory of nucleation and collapse stages was developed. Only the most general characteristics of the initial state of a system in which phase transitions take place are used in this description. The description of the collapse stage in the gradual metastability formation process is analogous to the description of its counterpart in the instantaneous formation of metastability. The only difference consists in that the transition of the bulk of matter from the metastable state, reached by the onset of the nucleation stage, to the stable state occurs while the metastability-inducing factors are still active.
The nucleation stage poses a most interesting and difficult problem for researchers studying phase transitions. In the theory of the nucleation stage, the questions of small system thermodynamics (for example, for small droplets and thin liquid films) are closely intermingled with the descriptions of the process of overcoming the energy barrier (which changes during the nucleation stage) by newly-formed stable phase particles, the growth peculiarities of these particles in a wide range of their sizes, and the correct interpretation of the collective effect of an ensemble of the growing stable phase particles on the state of initial metastable phase. Taken together with the effects of metastability-forming factors, this gives rise to a complicated, strongly non-linear mathematical problem. However, a remarkable feature of the conditions for the gradual formation of metastability consists in that the efforts to surmount mathematical difficulties are repaid by the discovery of interesting and even unusual nucleation properties. The most important of them is the weak dependence of the principal nucleation stage characteristics on the accuracy of measurements of thermodynamic parameters of small stable phase nuclei. It is this universal property that makes predictions of the theory under consideration quantitative and distinguishes it from the theory of nucleation after instantaneous metastable state formation which makes high demands upon the accuracy of the description of small critical nuclei.
The theory of the nucleation stage is most interesting for the heterogeneous mechanism, the most widespread in nature, by which stable phase nuclei (droplets) arise on foreign particles present in a supersaturated vapour volume. Such foreign bodies or heterogeneous centres can be ions, acid droplets, sea-salt crystals, dust or soot particles, etc. Given the great variety of properties and sizes of heterogeneous centres and the diversity of phase transition conditions, all attempts to construct a quantitative theory of heterogeneous nucleation may seem impracticable. For example, are sea-salt crystals completely dissolved in the droplets (formed of condensed vapour) which are of critical size that determines the nucleation rate? Is this solution saturated or not? Are insoluble aerosol particles totally or partially wettable? Does the critical size of droplets nucleated on wettable dust particles correspond to thin or thick liquid films? These unknown variables determine to a large extent such characteristics of the nucleation process as the number and average size of the droplets being formed or the duration of nucleation. In the gradual formation of metastability, the initiation and the duration of the nucleation stage depend not only on its rate but also on the internal processes in the nucleation system. Peculiar conditions of the gradual metastable state formation impose a certain degree of consistency between the sizes of nuclei whose thermodynamic parameters determine the nucleation rate and characteristics of heterogeneous centres around which these nuclei are formed. Such a consistency for the representative types of heterogeneous centres considerably simplifies the thermodynamic description of stable phase nuclei and leads to universal laws in the theory of heterogeneous nucleation.
The thermodynamics of heterogeneous nucleation has a rather long history. A key to build the thermodynamic relations is granted by finding the work of droplet formation of the chemical potential of condensing molecules in a droplet. The knowledge of the work of droplet formation or the chemical potential of condensate as a function of the number of condensing molecules (in the droplet) allows us to calculate all the thermodynamic characteristics of nucleation important for kinetics. The nucleation of a droplet on a macroscopic foreign particle may occur in two mechanisms. The first corresponds to formation of the thin liquid film, which uniformly covers the particle surface. This film grows as a whole by means of subsequent condensation until the macroscopic droplet is formed. The second mechanism realizes through the formation (at the particle surface) of separate small liquid lenses with finite contact angle. These lenses grow by means of condensation and are able to converge in the thick continuous film which grows as a single drop. The first mechanism is especially interested because it allows intensive nucleation at small vapour supersaturations. Evidently, the difference between the two mechanisms is provided by different wetting of the particle surface and by the particle size. In its turn, the wetting of the particle surface is determined by the surface forces at interfaces between solid and vapour, solid and the liquid film, the liquid film and vapour. Revealing the conditions for realization of these mechanisms and the description of the role of the surface forces in nucleation are the central tasks of the thermodynamics of heterogeneous nucleation on macroscopic particles. The density functional approach to description of small objects, like local density functional or local thickness functional (in the case of thin films), the equations of the Gibbs thermodynamics, molecular dynamics are the theoretical methods of modern statistical thermodynamics which are used to solve the nucleation problems.
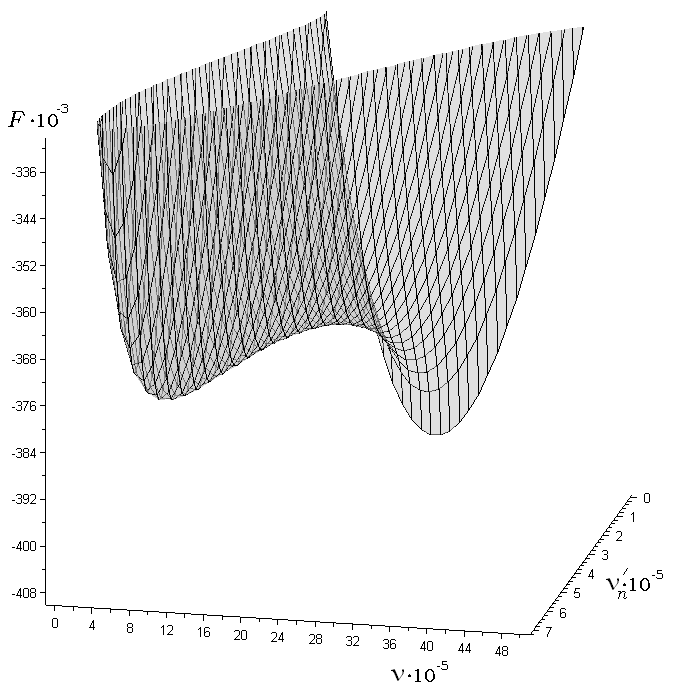
The
following figure can serve as an illustration to the aforesaid. This
figure shows the dependence of the work.
![]() (expressed in the thermal units
(expressed in the thermal units
![]() where
where
![]() is the Boltzmann constant and
is the Boltzmann constant and
![]() is the absolute temperature) of the formation of a liquid solution
film on the soluble particle of salt. The number of molecules of
water condensing in the film out the vapour is
is the absolute temperature) of the formation of a liquid solution
film on the soluble particle of salt. The number of molecules of
water condensing in the film out the vapour is
![]() .
The number of molecules of the salt remaining
in the particle residue in the droplet is
.
The number of molecules of the salt remaining
in the particle residue in the droplet is
![]() .
The figure depicts the situation in undersaturated vapour. The first
minimum of the work
.
The figure depicts the situation in undersaturated vapour. The first
minimum of the work
![]() corresponds to the thin stable film around the particle which
dissolves a little. The second minimum corresponds to the complete
dissolution of the salt particle in the droplet.
corresponds to the thin stable film around the particle which
dissolves a little. The second minimum corresponds to the complete
dissolution of the salt particle in the droplet.