Micellization

Micelles are the nanosized stable aggregates of surfactant molecules, which form spontaneously in surfactant solutions. With increasing the total surfactant concentration (i.e. the total amount of surfactant per unit volume of solution) above the first critical micelle concentration (CMC) the raction of micelles in the surfactant balance become yet significant. For the present, the range of applications of micellar solutions (containing a large number of micelles) is huge. They are used in detergents and for designing microemulsions, at ore mineral resources mining and oil production. Along with that, only a small fraction of the vast body of publications on surfactant solutions concern the kinetic of aggregation in micellar solutions, a fact that can be explained by the enormous complexity of micellization processes. The pioneering studies of micellization kinetics were motivated by the desire to gain insights into the experimentally observed stages of the slow and fast relaxation of micellar solution with spherical micelles. The concept of the stepwise growth of micelles proposed by Aniansson, by analogy with homogeneous nucleation, became widespread and has been used to describe more complex systems. Based on the concept of aggregation as a process involving the overcoming of a barrier, this approach stopped short of fully using the methodology of the nucleation theory in establishing relationships between the main characteristic of aggregation, properties of molecular aggregates of various sizes, and the parameters of the initial and final states of the micellar solution. Since experimental information on premicellar aggregates, especially critical nuclei of micelles, was limited at that time, the development of the kinetic theory of aggregation slowed down.

In recent years, however, a revival of interest in the kinetics of micellization has been observed. The papers where the stepwise aggregation scheme based on the Becker–Döring kinetic equation was examined to find out whether this scheme described irreversible behavior and provided stable solution. As a result, a simplified calculation procedure was proposed, which made it possible to optimize the algorithms for solving the system of kinetic equations of aggregation. Advances in the nucleation theory, in particular, in solving the problems of ion-induced nucleation and heterogeneous nucleation on wettable particles (processes which appear to be similar to micellization), have also been made.

To construct a kinetic theory of micellation in surfactant solutions, it is necessary to know the thermodynamic characteristics of formation of a molecular surfactant aggregate (work of aggregation). There are two thermodynamic models of micelles. Under conditions, when the total surfactant concentration exceeds the first CMC but is lower than the second CMC (beginning with which a considerable fraction of the surfactant forms cylindrical micelles), these models show that the work of aggregation as a function of the aggregation number has not only a hump but also a well (to the right of the hump) after which the work of aggregation tend to infinity with increasing aggregation number. The existence of the hump and well in the aggregation work–aggregation number dependence make the kinetic theory of micellization more complex than the kinetic theory of homogeneous nucleation, in which the work of formation of a nucleus as a function of the number of constituent molecules has only a maximum, monotonically decreasing to either side of it. Even more complicated situation arises, when the total surfactant concentration exceeds the second CMC and cylindrical micelles begin to play an increasing role, and the additional potential hump and well appear in the aggregation work.

As in the kinetic theory of nucleation, an important characteristic of the kinetic theory of micellization is the fluctuation-driven flux of molecular aggregates through the hump from the region located to the left from it. However, since the aggregation work–aggregation number dependence for micellar solution has a well after the hump, the reverse fluctuation-driven flux from the well becomes important. The determination of the direct and reverse fluxes of molecular aggregates through hump (barrier to aggregation) plays a key role in constructing kinetic models of aggregation in analyzing the stages of micellization.

The important task of the theory of micellization are the kinetic description of micellar relaxation and revealing of the hierarchy of characteristic times of micellization.This hierarchy gives a graphic representation of the relative values of the characteristic times of formation and decay of micelles and of the complex, multistage process of approach of the micellar solution to the final state of equilibrium.

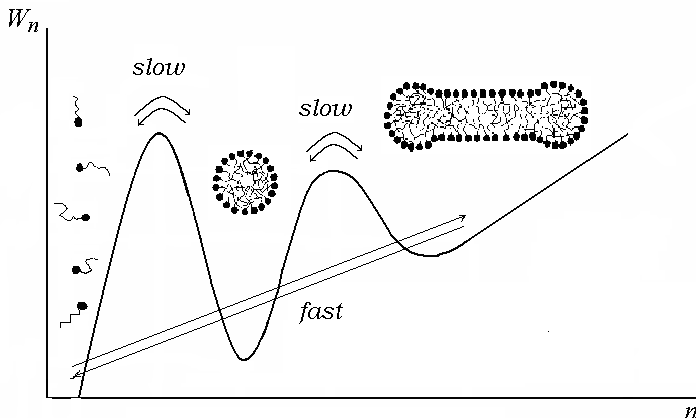
The following figure can serve as an illustration to the properties of the micellar solutions. This figure shows the work (expressed in the thermal units ) of the formation of an aggregate of surfactant molecules as a function of the number of molecules in the aggregate at concentration above the second CMC. The regions of surfactant monomers and that of spherical and cylindrical micelles are indicated with corresponding pictures. The arrows show the direct and reversal transitions referred to fast and slow processes in the micellar solution.